AT_abc344_e 题解
本文同步发表于洛谷。
赌狗天天输的一集。
赛时各种【数据删除】原因导致没做出来。
大意
给你一个长度为 \(N\) 的序列 \(A=(A_1,\ldots,A_N)\)。保证 \(A\) 中的元素是不同的。
你要处理 \(Q\) 个操作。每个操作是以下两种类型之一:
1 x y:在 \(A\) 中元素 \(x\) 后面紧接着插入 \(y\)。当给出此查询时,保证 \(x\) 存在于 \(A\) 中。2 x:从 \(A\) 中删除元素 \(x\)。当给出此查询时,保证 \(x\) 存在于 \(A\) 中。
保证在处理完每一个查询后,\(A\) 都不是空的,并且其元素都是不同的。
处理完所有查询后,打印 \(A\)。
一句人话:模板双向链表。
思路
不知道链表的可以学一下单向链表,B3631。
单向链表大致长这样: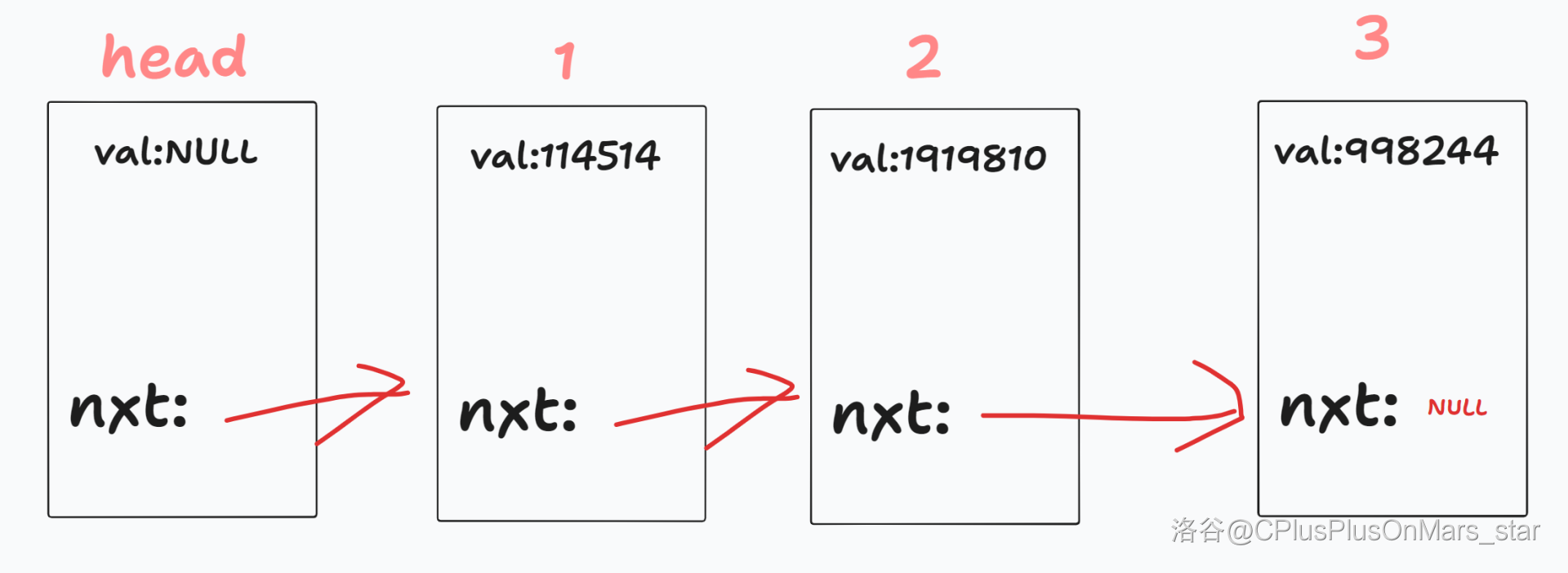
但是!我们的主角双向链表他有出息!他两边都能指!
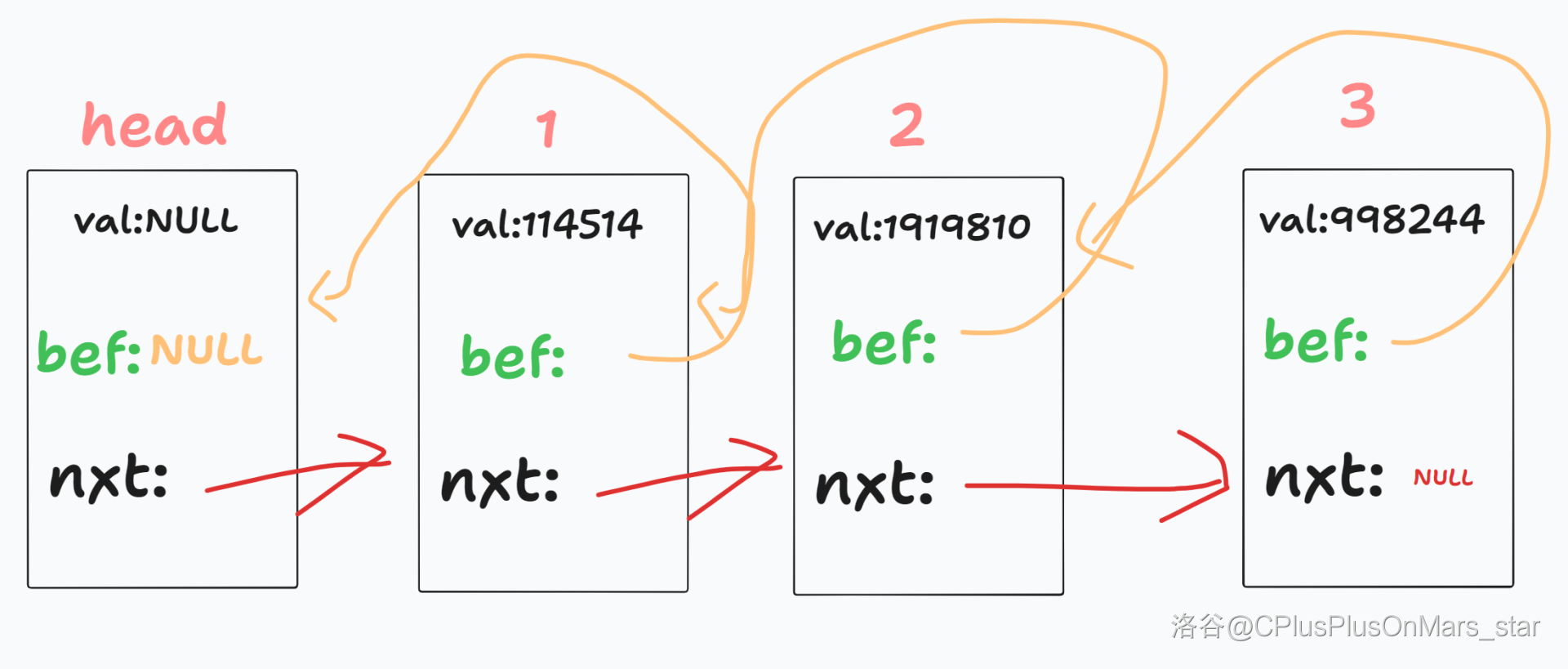
然后,我高高兴兴的写代码(很简单,按照题面直接做就行),直接就超时了。
我蒙了,为啥?发现是从 head 调到对应位置太耗时间了。
诶,有没有注意到题面说了“保证 \(A\) 中的元素是不同的。” 和“保证在处理完每一个查询后,\(A\) 都不是空的,并且其元素都是不同的。”?
我不要离散化!\(10^9\) 直接 map 启动!
然后代码木大木大了很久还是不对,后来发现是添加的时候忘记更新 x.bef 了…
代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 1000010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define i128 LL
#define lowbit(x) ((x)&(-(x)))
#define lc (u<<1)
#define rc (u<<1|1)
using namespace std;
void read(i128 &x)
{
i128 f=1;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
}
void write(i128 x)
{
if(x>=10)write(x/10);
putchar(x%10+'0');
}
LL n,a[200010],q,op,x,y,o;
struct nod
{
LL v,nxt,bef;
}l[400010];
map<LL,LL>f;
int main()
{
cin>>n;
l[0].nxt=1;
rep(i,1,n,1)
{
cin>>a[i];
l[i].v=a[i];
l[i].nxt=i+1;
l[i].bef=i-1;
f[a[i]]=i;
}
o=n+1;
cin>>q;
while(q--)
{
cin>>op;
if(op==1)
{
cin>>x>>y;
LL t=f[x];
l[++o]=(nod){y,l[t].nxt,t};
l[l[t].nxt].bef=o;
l[t].nxt=o;
f[y]=o;
}
else
{
cin>>x;
LL t=f[x];
l[l[t].nxt].bef=l[t].bef;
l[l[t].bef].nxt=l[t].nxt;
f[x]=0;
}
}
nod u=l[l[0].nxt];
while(u.v!=0)
{
cout<<u.v<<' ';
u=l[u.nxt];
}
return 0;
}
闲话
赛后突然想起一个东西:
我【数据删除】!有个玩意叫
list…
我是消愁。
代码就不放了,STL 真的简单。